
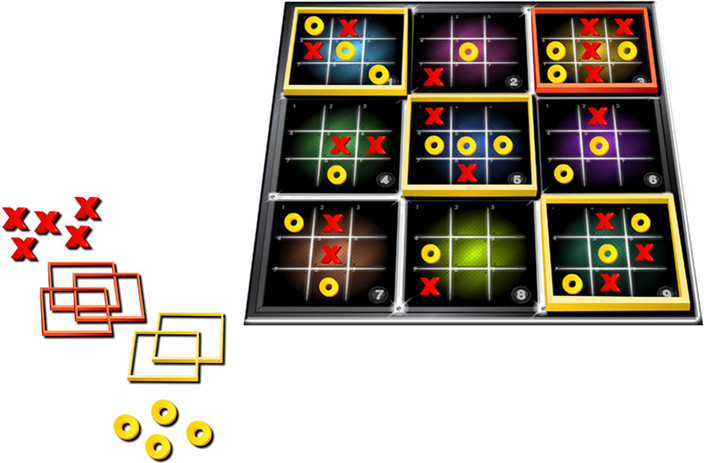

In all other positions, the score is the number of small boards won minus the number of small boards lost.Ģ) Our second heuristic (heur2) takes into consideration many more features of the given board: small board wins add 5 points, winning the center board adds 10, winning a corner board adds 3, getting a center square in any small board is worth 3, and getting a square in the center board is worth 3. An alpha-beta agent of depth 3 won 69.5% of games played against a player of depth 2 (n=100 p-value<10 -4) and 75.5% of games played against depth 1 (n=100 p-value<10 -6).ġ) Our simple heuristic (heur1) evaluates winning and losing with high absolute values: 10,000 for a winning position and -10,000 for a losing position. How important is search depth? An alpha-beta agent of depth 2 won 79.8% of games against an alpha-beta agent of depth 1 (n=1,000 p-value<10 -80). When testing an expectimax agent against a minimax agent with depth of 2 and heur3, the minimax agent won convincingly with 78% of games (n=100 p-value<10 -7). Indeed, when running an expectimax agent against a random agent, it won 100% of the time (n=100 p-value<10 -30), better than minimax agents which also tied and lost some games. Their speeds were quite different - when comparing agents of depth 2, the minimax agent took an average of 1,033 milliseconds to make a move, against just 55 milliseconds for an alpha-beta agent (n=10).Įxpectimax agents should be better against random agents, but since our minimax agents already defeat random agents, this is not such a big advantage. Indeed, when comparing an alpha-beta agent to a minimax with the same heuristic and depth, the results were 49.6% wins for the minimax agent (n=1,000 =0.098 p-value=0.7542), so the agents are indeed similar in strength. An Alpha-Beta agent using the heur3 and a depth of 2 won 99.4% of games (n=1,000 p-value<10 -280) against a random agent.Īlpha-beta agents should return identical results to minimax agents, only faster. A very basic Alpha-Beta agent using the simplest heuristic (heur1) and a depth of 2 won 96.35% of games (n=10,000 p-value<10 -320) against a random agent. Depth is denoted using the Berkeley notation, where a single search ply is considered to be a move for each player.Ī random agent was easily defeated even by the simplest agents. The game tree is too deep for these algorithms to traverse in reasonable time, so heuristics are used to approximate the value of nodes of a certain depth. (We used the Berkeley AI course assignments as a basis for several stages of the project.) We used three basic search algorithms to traverse the game tree: the Minimax algorithm to traverse the whole tree, the Minimax algorithm with alpha-beta pruning to decrease the number of paths observed by the algorithm, and the Expectimax algorithm, which takes the expectation of the other player's values instead of their minimum. We will use a proportion test with a confidence level of 0.95, and accept if the p-value of Pearson's chi-squared test statistic for 1 degree of freedom is larger than the commonly accepted threshold of 0.05. minimax and alpha-beta), so our null hypothesis will be that they are unequally proportioned. In other cases, we will want to test the hypothesis that two players have the same strength (e.g. Tied games are counted as a half-win for each player. We use the two-tailed variation of the binomial test to test if either player is better. Our null hypothesis will usually be that the players have equal strength and will therefore win an equal number of games. The starting player will be chosen randomly for each game. 1 In each evaluation of two agents, we will present n (number of games played), the percentage of games won by each player, and the p-value of the results. Because it is an exact statistical test of the statistical significance, we can get accurate p-values and not just approximations. To evaluate the different agents used in the project, our main statistical tool will be the binomial test. If all squares in the small board have been exhausted, or if the board has already been won, the player may choose to make his move anywhere on the board. In this example, the blue player played the top-right square in the bottom-left small grid, so the red player must now play his turn in the top-right board (colored in yellow).


 0 kommentar(er)
0 kommentar(er)
